BALANCEO DE CIRCUITOS DE DISTRIBUCIÓN PRIMARIA

 

 

Resumen- Se presentan los resultados de aplicar un método de balance de los circuitos de distribución primaria. El balance se realiza desde el último usuario a la subestación pasando  transformadores conectados a la fase más cargada hacia la menos cargada, eligiendo el conjunto que más contribuya con el balance ideal. Primero se pasan ramales monofásicos completos y después se estudian los ramales de tres conductores haciendo permutaciones de fase o cambiando el ramal completo desde el tronco de acuerdo al aporte que hagan en el proceso de balance. Se presenta un ejemplo de un circuito “desbalanceado” utilizando un programa de computación elaborado por los autores  para estudio de redes de distribución que realiza esta función.

Introducción

Las redes de distribución primaria brindan servicio a las cargas trifásicas y monofásicas utilizando transformadores monofásicos independientes y bancos de dos o tres transformadores así como transformadores trifásicos. La energía es transportada a través de ramales que pueden tener uno, dos, tres y cuatro conductores. La diversidad de cargas a servir desde las fases del circuito puede llevar a circulación de corrientes por cada una de las fases del circuito que difieran mucho entre ellas provocando pérdidas y caídas de voltajes innecesarias. El balance de las corrientes en las fases de un circuito se debe realizar, en primera instancia, garantizando que las capacidades de transformadores conectadas a cada una de ellas sea del mismo orden. Por otra parte, se trata de llevar los transformadores a un nivel de carga que se encuentre en un rango normado buscando la eficiencia de trabajo de los equipos. Si esto se logra, se puede asegurar que balanceando la carga conectada a cada fase, se tendrá un balance aceptable en el circuito. El objetivo  de este trabajo es presentar un método para realizar la evaluación del balance de cargas por fases en un alimentador primaria y los resultados de algoritmo incorporados a un programa de computación elaborado con estos fines.

 

Desarrollo

 

El balance de cargas por fase en los circuitos primarios de distribución es una mejora organizativa básica; se debe realizar, muchas veces, antes de proceder a  otros estudios puesto que los métodos mas utilizados suponen que los circuitos que se estudian ya han sido balanceados. Se puede balancear la carga asignada a cada fase si se conoce la demanda pero si se realizan procesos de estimación de la distribución de la demanda se puede balancear la capacidad instalada como se describe en este artículo. Existen normas que establecen  la máxima diferencia entre la corriente por las fases; por ejemplo, en muchas empresas se establece que la máxima diferencia entre la fase mas cargada y la menos cargada no debe sobrepasar el 10 % y en otras hasta el 20 %.

 

Aspectos Generales

 

En todos los casos se busca que la carga que se pase de una fase a otra mejore el balance existente. Son designadas las fases y su carga como:

 

FaseMasCargada ,  kVAMasCargada.

FaseMedia, kVAMedia.

FaseMenosCargada, kVAMenosCargada

 

Sea  Desbalance = ( kVAMasCargada- FaseMenosCargada) e Ideal = Desbalance/2.

 

Clasificación de los nodos. Los nodos se clasifican en cuatro grupos. Un nodo i toma siempre el valor de la variable Analizado(i)  dependiendo del tipo de ramal y si se quiere evaluar ahora o no.

 

Analizado(i)= 1 Ramal con uno o dos conductores

                    =  2 Ramal con dos fases y neutro

                    =  3 Ramales con tres fases

                    =  5 Cuando no debe participar en el análisis de cambio de fases  que se está haciendo en ese momento.

 

Estudio de ramales monofásicos. En el circuito existen n1 ramales de este tipo, el algoritmo que se desarrolla busca la combinación de p ramales; p=1, 2, ... , n1 que minimice el desbalance respecto al actual. En general las combinaciones posibles dependen del valor de p

 

 C n1,p = ( n1*(n1-1)*...* (n1-p))/ p!; para p = 1,2,…, n1

 

Algoritmo:  Si  LoMejor son los kVA que más aumenten el balance hasta el momento:

 Se toma  k = 1, 2, ... n1 ( total de ramales monofásicos).

Para fijar el primer nodo de un ramal k, Se busca el Nodo(k) como el # del nodo que sale de un ramal de tres fases, siendo Selecto(k) = NodoBase(1) designado como el  nodo de un ramal trifásico que envía energía al Nodo(k) de la fase mas cargada.

Sea kVA(selecto(k)) los kVA instalados en el ramal y Fase(k) la fase más cargada.

  kVAen(k) es la carga conectada al ramal

  Si LoMejor – Ideal > kVAen(Selecto(k)) – Ideal mejora el balance

 Se hace LoMejor = kVAen(Selecto(k)  y  NodoBase(1) = Selecto(k)

 

Quiere esto decir que “LoMejor” se va guardando en una variable y el NodoBase  guarda el Número del nodo que alimenta al ramal correspondiente. Al final queda el ramal que más  contribuye al balance.

 

El análisis se continúa tomando dos, tres, cuatro o cinco ramales que cambien de fase a la vez. En cada caso, la cantidad de combinaciones posibles se traduce en un conjunto de (p)  lazos; por ejemplo, para el paso de cinco (5) ramales de un circuito de n nodos:

Si n ³ 5 entonces:

k = 1,...,n-4	l=k+1,..., n-3	m= l+1,…, n-2
p=m+1,, n-1	q = p+1,…,n

 

Tomar kVASuma =  kVAen(Selecto(k)) + ... + kVAen(Selecto(q))

Si LoMejor – Ideal  >  kVASuma – Ideal  mejora el balance.

LoMejor = kVASuma;  NodoBase(1)= k; NodoBase(2)=l;..., NodoBase(5)=q

 

De esta forma se escoge la cantidad de ramales que más contribuyen al balance.

Ahora hay que reajustar las fases de acuerdo a los resultados y evaluar la FaseMasCargada, FaseMedia y FaseMenosCargada y la carga conectada a ellas.

 

Balance de los ramales de dos fases y neutro.  Estos ramales pueden servir cargas monofásicas y trifásicas; se realizan dos procesos de balance en ellos: Cambio de fases de todo el ramal e intercambio de fases de cargas individuales. El procedimiento es el siguiente:

 

1º. Se busca el inicio de cada ramal a partir de Analizado(i) y se halla la carga de todo el ramal por fases.

2º. Si la diferencia entre la carga de las fases del ramal es menor que el “desbalance“ total entre ellas, se hace el cambio de fases. Ejemplo, si :

En Total KVAFase A = 600 kVA  y kVAFaseB= 500 kVA  y

En el ramal kVAdeA = 110 kVA y kVAdeB= 70 kVA; al conmutar las fases mejora el balance en 80 kVA; es decir quedan

KVAFase A = 560 kVA  y kVAFaseB= 540 kVA  .

Dentro del ramal se evalúan ahora las cargas individuales evaluando la diferencia entre las Fases y comparándola con la diferencia total del circuito; si es menor, se intercambia la conexión de fases de la carga.

 

Balance de ramales de tres fases. Si fuera necesario, se evalúan las cargas monofásicas de ramales trifásicos utilizando por un procedimiento similar al de ramales monofásicos pero la carga equivalente del ramal es la carga del nodo trifásico.

 

En la figura a seguir se presenta un circuito de 23 nodos, la capacidad instalada  por fases se muestra en la tabla de la parte inferior.

 

 

 

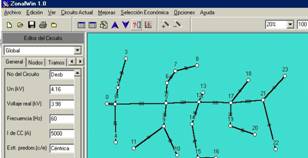
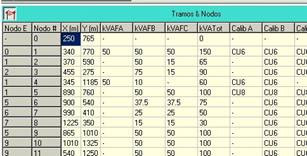
En el análisis de estado actual  se puede observar el nivel de desbalance del circuito, estando  más cargada  la fase B y menos cargada la fase A. Estando  más cargada  la fase B y menos cargada la fase A.

 

 

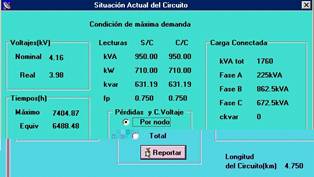
Se selecciona la opción de mejora Balance del Circuito. El balance de ramales monofásicos se muestra en la siguiente ventana.

 

 

Se decide pasar al balance de ramales de dos fases y el resultado es el siguiente:

Ya el nivel de balance es aceptable (8,1 %). En resumen, fueron cambiados de fases: tres ramales monofásicos y cuatro  ramales de dos fases.

 

Conclusiones  

 

Se desarrollaron los procedimientos para realizar el balance de los circuitos de forma automatizada siguiendo una secuencia de análisis de ramales desde el extremo de los circuitos hasta la subestación, conmutando los ramales monofásicos que se encuentran en la fase más cargada hacia la fase menos cargada que de conjunto más contribuyan al balance, ajustando los ramales de dos fases y neutro con el mismo criterio y si fuera necesario cambiando de fases las cargas monofásicas de ramales trifásicos hacia la fase más cargada. La cantidad de permutaciones que deben evaluarse es grande pero el orden establecido en el algoritmo y la velocidad de cálculo que permiten las máquinas actuales posibilitan que los resultados sean inmediatos.

 

Bibliografía

 

[1]   Pansini A., Basic Electrical Power Distribution. Vol 1, Rider Publisher, Inc. 1958.

[2]   González M., Matemática  Superior. 1957.

[3]   Varios, Consulta a Ingenieros de la Empresa Ciudad de la Habana. UNE

 

Biografías

 

Raúl Carvajal Pérez, Doctor en Ingeniería, actualmente es Profesor del ISPJAE (Cuba). Profesor visitante del Programa de Maestría en Sistemas Eléctrico de Potencia en la UTO, 2002.

 

David Ismael Rojas, Ingeniero Eléctrico, UTO (1990), Master of Science, Universidad de Santa Catarina, Brasil (1994). Actualmente es docente de la FNI y Coordinador del Ciclo Básico.

 

Sus áreas de interés: dinámica de sistemas de potencia.

 

e-mail: [email protected]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Dir: León No. 335 y Pagador

Telf: 2-5113473 Fax: 5241113-54497

Cel: 71841818

 

Oruro – Bolivia