Modelado mediante bond graphs. Caso de estudio: servomecanismo
Stella Vallejos Vargas Ramiro Franz Aliendre García
Resumen- En este trabajo se muestra como aplicar la técnica de los diagramas de enlace de energía (bond graphs), a un sistema de tipo electromecánico, con el fin de obtener el modelo matemático del mismo. Esta técnica constituye un enfoque estructurado de modelización de los sistemas dinámicos, lo que hace que sea una herramienta importante al momento de modelar sistemas.
Palabras clave: Bond graph, diagramas de enlace de energía, sistema de posición
INTRODUCCIÓN
|
L |
as analogías existentes entre sistemas, y las ecuaciones de balance de energía, son la base para la introducción de los bond graphs; los procesos que son modelados realizan un intercambio de energía y conservación de la misma, así la modelización es realizada mediante el seguimiento del flujo de energía en el sistema.
Los bond graphs en esencia capturan los intercambios de energía, cuantificándolos instantáneamente según la potencia en juego en el sistema. Entre sus principales características y ventajas, se cuentan las de ser un lenguaje gráfico, acausal en principio y de formulación independiente de las alinealidades presentes en el sistema.
El bond es una línea horizontal, interpretada como una conexión entre subsistemas que intercambian energía. La arista de esta línea horizontal, marca la dirección en la que va la energía.
FIGURA I
Bond
![]() e
e
f
Un sistema físico dinámico puede pensarse como una porción delimitada del universo en la que a cada instante se verifica un intercambio y balance de potencia entre todos los elementos que lo componen. Bond graphs distingue clases elementales de componentes en función del procesamiento que estos hacen de la energía [2],[1].
Las variables físicas son generalizadas en cuatro tipos: [2]
1) Variables de potencia: esfuerzo “e” y flujo “f”, su producto da potencia
2) Variables de energía: momento “p” y desplazamiento “q”, son las respectivas integrales de las dos anteriores. La energía en los almacenadores es una función de ellas.
La tabla I muestra las variables de energía y potencia en función al dominio físico del sistema. [2]
|
Dominio físico |
Variables de potencia |
Variables de energía |
||
|
Esfuerzo e |
Flujo f |
Momento p |
Desplaz. q |
|
|
Traslación |
Fuerza |
Velocidad |
Impulso |
Desplaz. |
|
Rotación |
Torque |
Velocidad Angular |
Momento Angular |
Ángulo |
|
Dinámica de fluidos |
Presión |
Caudal |
Impulso del fluido |
Volumen |
|
Electro-magnetismo |
Tensión |
Corriente |
Flujo magnético |
Carga eléctrica |
|
Química |
Potencial Químico |
Flujo molar |
|
Número de moles |
|
Termo-dinámica |
Temp. Absoluta |
Flujo de entropía |
|
Entropía |
TABLA I
Variables Físicas
Todo sistema, en general, tiene una entrada que es una señal generada externamente. En bond graphs son llamadas fuentes, y pueden ser de dos tipos dependiendo que la entrada sea esfuerzo o flujo. En los diagramas de enlace de energía una fuente de esfuerzo viene representado por Se , y una fuente de flujo es representada por Sf.[1]
Los vínculos son una parte muy importante en los bond graphs, estos son de tipo multipuerta (admiten varios enlaces adyacentes), y representan las estructuras mas simples como, esfuerzo común (p) y flujo común (s).
Dicho de otra manera, todos los enlaces asociados a un vínculo (p) tienen asociada la misma variable de esfuerzo, y todos los enlaces asociados a (s) tienen asociada la misma variable de flujo. En el domino eléctrico un vínculo (s) significa corriente común y representa la estructura de un circuito serie, mientras que un vínculo (p) significa tensión común y representa la estructura de un circuito paralelo.[1],[2]
El vínculo serie esta caracterizado por el mismo flujo:
![]()
La sumatoria algebraica de los esfuerzos igual a cero
![]()
Análogamente el vínculo paralelo cambia los roles para el esfuerzo y el flujo, por tanto se tiene ahora el mismo esfuerzo:
![]()
La sumatoria algebraica de los flujos igual a cero
![]()
Otro elementos componentes son los almacenadores que pueden ser de dos tipos:
El capacitor C es la generalización de un almacenador de energía potencial. Este elemento puede representar un tanque de agua, un resorte mecánico, etc. [2]
La inercia I, generalizada como un almacenador de energía cinética, físicamente representa a la inductancia eléctrica, la inercia mecánica, etc. [2]
Finalmente, entre los elementos del bond graph se encuentran los disipadores que son representados por la letra R y físicamente representan el rozamiento en mecánica, la resistencia eléctrica en la teoría de circuitos y los diferentes componentes análogos en los demás dominios de la física. [2]
En algunos casos los bond graphs pueden ser reducidos al igual que los circuitos eléctricos. A continuación se muestran dos ejemplos de ésta característica [1].
1) Vínculos que tienen solo dos bonds (las aristas apuntan en el mismo sentido).
FIGURA II
Simplificación en bond graph
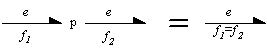 |
|||
2) Una directa aplicación es que dos vínculos adyacentes de la misma clase pueden ser absorbidos y convertirse en uno solo.
FIGURA III
Simplificación en bond graphs
 |
 |
||
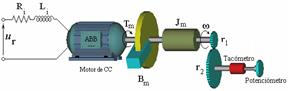
El sistema de control de posición angular considerado en este artículo, utiliza un motor de corriente continua como actuador. En el servomotor del sistema, el campo magnético es producido por excitación constante, es decir el flujo magnético es independiente de la corriente de armadura. De este modo el control del servomotor se realiza mediante la corriente de armadura, o mejor mediante la tensión de armadura. El motor posiciona la carga mediante un tren de engranajes. Un potenciómetro, cuyo movimiento se realiza junto con el eje del disco a través de un tren de engranajes de relación 1:1, sirve de sensor y convierte la posición angular de la carga mecánica, en una señal eléctrica proporcional de tensión. La señal de tensión de entrada representa la posición angular deseada (entrada de referencia o setpoint) de la carga mecánica. El sistema posee también un tacogenerador cuya tensión de salida es proporcional a la velocidad de rotación de la carga mecánica.
FIGURA IV
Sistema de Posición de Laboratorio
 |
El sistema estudiado es de tipo electromecánico. Puede ser dividido en tres partes: en la primera se encuentra el motor de corriente continua, en la segunda el tren de engranajes que posiciona la carga mecánica, y la tercera parte pertenece al sistema de medición. La estructuración del bond graph, será realizada tomando en cuenta cada una de estas partes.
La excitación del sistema está dada por la tensión de armadura en el motor de corriente continua, por lo tanto la entrada es una fuente de esfuerzo. Este esfuerzo será repartido en el sistema eléctrico, como caída de tensión en la resistencia y en la inductancia para obtener al final una fuerza contraelectromotriz, que será transformada a través de la ganancia k1 en la velocidad angular del motor. Por estas razones el bond graph del motor de corriente continua es el siguiente:
FIGURA V
Bond graph del motor de c.c.
 |
Una vez transformada la energía eléctrica en energía mecánica, el motor posiciona la carga mecánica mediante un tren de engranajes por lo tanto la velocidad angular (flujo) será la misma, debido a esto se empleará un vínculo s; análogamente al sistema eléctrico el esfuerzo obtenido en el eje del motor se dispersa en la inercia mecánica y el rozamiento, consecuentemente el bond graph es el siguiente:
FIGURAVI
Bond graph del motor del c.c. mas el tren de engranajes
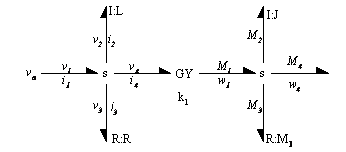 |
El sistema de medición del servomecanismo está compuesto por un tacómetro y un potenciómetro, mediante estos se obtiene la señal de tensión proporcional a la velocidad y la posición. Con la teoría de bond graphs, ésta conversión se realiza a través de ganancias que para este caso de estudio son k2 y k3. Sus significados físicos están expuestos abajo. El motivo para emplear un conversor de energía, como lo es GY, es para realizar la transformación de energía mecánica a eléctrica; mientras que el transformador TF es empleado en la siguiente etapa del bond graph para realizar una transformación de tensión a tensión a través de la ganancia k2.
Finalmente el diagrama de enlaces de energía para el sistema de posición angular es:
FIGURA VII
Bond graph del servomecanismo
 |
Las ecuaciones que describen la dinámica del sistema son derivadas del diagrama de enlace de energía de la siguiente forma.
La primera columna representa un análisis hacia adelante y la segunda un análisis hacia atrás, del diagrama de enlaces de energía del servomecanismo.
Paso Adelante Atrás
1 ![]()
![]()
2 ![]()
![]()
3 ![]()
![]()
4 ![]()
![]()
5 ![]()
![]()
6 ![]()
![]()
7 ![]()
![]()
8 ![]()
![]()
9 ![]()
![]()
donde:
va: Tensión de referencia (proporcional al ángulo deseado)
i1: Corriente de armadura
w1= w2= w3= w4 : Velocidad angular del eje del motor
f: Posición angular del eje del motor
J: Momento de inercia que actúa sobre la carga mecánica
Bm: Coeficiente de fricción viscosa
R: Resistencia de armadura
L: Inductancia de armadura
M1: Torque motor
k1: Constante proporcional de la f.c.e.m. y la velocidad angular del motor
k3 * k1: 1
k2: Constante de transformación entre la tensión de velocidad y la tensión de posición
La primera variable de estado representa la caída de tensión en la inductancia, la segunda representa el par en la inercia mecánica, análogamente la variable primera y la segunda variable representan esfuerzo. La tercera variable representa la velocidad angular obtenida por el movimiento del motor
![]()
![]()
![]()
![]()
![]()
![]()
Eliminando las variables que no son estados en las ecuaciones obtenidas del diagrama de enlaces de energía, se obtiene:
Primera ecuación de estado:

![]() (1)
(1)
![]()
Segunda ecuación de estado:
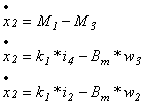
![]() (2)
(2)
Tercera ecuación de estado:
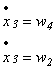
![]() (3)
(3)
La salida en función de las variables de estado es:
![]()
![]() (4)
(4)
De las ecuaciones (1), (2), (3) y (4) se obtiene:
 (5)
(5)
![]() (6)
(6)
De (5) y (6):
 (7)
(7)
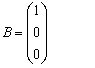 (8)
(8)
![]() (9)
(9)
Mediante
![]() (10)
(10)
Reemplazando (7), (8) y (9) en (10); la función de transferencia de sistema de posición angular es la siguiente:
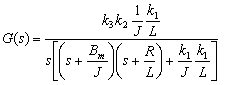 (11)
(11)
La función de transferencia en (11), expresada en constantes de tiempo es la siguiente.
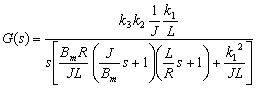 (12)
(12)
En (12), la constante de tiempo eléctrica L/R del sistema es bastante pequeña con relación a la constante de tiempo mecánica, por lo tanto la función de transferencia se puede reducir a:
 (13)
(13)
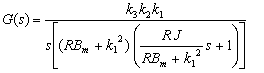 (14)
(14)
De la expresión (14), la ganancia y la constante de tiempo del sistema son:
![]()
![]()
Quedando el modelo del servomecanismo como:
![]()
Bond graph representa un método sistemático para el modelamiento de sistemas, además tiene la ventaja de estar basado en los conceptos físicos de energía, lo cual hace que la misma metodología sea usada para diferentes tipos de sistemas
Trabaja localmente es decir “una unión a la vez” de esta forma sistemas complejos pueden ser resueltos por esta metodología.
Bond graph da una completa descripción del sistema dinámico y puede automáticamente ser representado en ecuaciones de estado.
Referencias
[1] Lennart Ljung and Torkel Glad, “Modeling of Dinamic Systems”, Prentice Hall, 1994
[2] “Un ambiente computacional para modelización de sistemas dinámicos no lineales con Bond Graph”. Disponible en: www.eie.fceia.unr.edu.ar/~ekofman/files/paper_rpic99.pdf -
[3] “Preparation of papers for IEEE transaction on magnetics” IEEE Transl. J. Magn. Jpn., vol. 2, pp. 740-741, August 1987 [Dig. 9th Annual Conf. Magn. Jpn., p. 301, 1982].
[4] Katsuhiko Ogata, “Ingeniería de Control Moderno”, Prentice Hall, 1996
[5] Benjamín C. Kuo, “Sistemas de Control Automático”, Prentice Hall, 1996.
[6] D’azzo , “Sistemas de Realimentacion”, Paraninfo,1980.
Stella Vallejos Vargas. Nacida en Oruro - Bolivia en diciembre de 1979. Graduada por excelencia de la Universidad Técnica de Oruro, Facultad Nacional de Ingeniería, julio de 2002, como Licenciada en Ingeniería Eléctrica.
Actualmente se encuentra desarrollando su proyecto de grado: Control GPC para un sistema de posición, para optar a la Licenciatura en Ingeniería Electrónica, por la Universidad Técnica de Oruro.
Ramiro Franz Aliendre García. Ingeniero eléctrico por la Universidad Técnica de Oruro – Bolivia, Master en Ciencias por la Universidad Mayor de San Simón, Cochabamba – Bolivia. Realizó su tesis de maestría en una pasantía académica en la Universidad Federal de Santa Catarina, Florianópolis – Brasil. Fue invitado a una pasantía de investigación en la Technical University of Delft, Holanda, en el año 2001. Fue profesor invitado por la Universidad Eduardo Mondale, Maputo, Mozambique. Actualmente es docente a tiempo completo en la Carrera de Ingeniería Eléctrica y Electrónica de la Facultad Nacional de Ingeniería, Universidad Técnica de Oruro, Bolivia. Es también asesor de la rama estudiantil de la misma universidad.
Áreas de interés: controladores PID, control predictivo, automatización industrial.
